I’m going to warn you now; this will involve maths. In fact, it's going to involve statistics, which I’m given to understand most people abandon shortly after being deeply confused at about age 16. One of the things people don’t generally know about psychologists is that most of them have had to get up to post graduate level in statistics, and some of them NEVER STOP. Scary. Personally, it’s left me with a lingering lust for large data sets and seas of numbers to swim in, plus a tendency to read the OK Cupid blog and XKCD and find them both witty and entertaining.
Anyway, why is this relevant? Oh yes, because it’s a fact not universally acknowledged that most people are in business to make money. Yes yes, I know, everyone’s strapline or vision statement or whatever in fashion is about the sort of woman you want to be, what awesome power they bring to the world, or the amazing artistry involved in their production techniques, and all those things are valid, but trust me, basically, stuff got to pay the bills or it ain’t happening.
For said bills to get paid, you need turnover (the amount of sales you make overall), profit (your overall sales minus your overall costs) and cashflow (not buying lots of stuff that then sits about for ages, because there’s an intrinsic cost in stuff just sitting about, plus, you spent all your money on it and now have nothing to live on).
Statistics are what helps you work out what sizes to do so that you make the most sales the fastest, without too much stuff sitting about.
To understand how this works, we’re going to have to do a stats lesson. Take a nice relaxing breath now if you’re allergic to this stuff, and be happy, because I don’t actually like numbers. Welcome to my world of badly drawn graphs and guesstimated numbers. Badly drawn because my ability to use computers to produce graphics is nil – I have Morgana for that – and guesstimated because I am quite bad at sums and anyway, there’s no bonus to us in everyone knowing our exact figures. You can blame Made By Niki for convincing me that badly drawn graphs were acceptable on a vaguely professional blog. Possibly this was industrial sabotage.
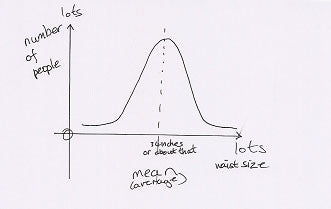
So, basic stats. When you have a large population, that is, a group of things or people, anything you might care to measure about them, when you put it on a graph, tends to produce this shape:

We call this a symmetrical distribution. It used to be called a normal distribution, but people get a bit peculiar about the word “normal”, and before that it was called the bell curve, but then someone wrote a book entirely full of right wing crazy called that, so the general consensus was we’d walk quietly away from that term. I think proper mathematicians call it a Gaussian distribution.
Let’s imagine this one is the waist size of adult women in the UK. There aren’t very many people with very tiny or very large waists, and obviously, no-one has a zero waist measurement. Most people are somewhere in the middle. In fact, due to the magic that happens when you work with big lots of numbers, 68% of people are in the middle (go and read about standard deviation if you want that explained). We think the average UK dress size is a 14-16, although there’s no great agreement on what exactly that means, but it's somewhere around the 32-34 inch mark.
But what does “average” mean? There are 3 types of average. The arithmetic mean is when you add up each value in a group – let's say I have 5 women, I add the 5 waist sizes and then divide by 5 to get to get the mean. The mode is the most frequent value – so the same 5 women, if two or more have the same waist measurement, then that’s the mode.
The median is the value where half the people are above it and half below – so in my 5 women, it would be the one that two people were smaller than and two people were bigger than (sort of; there’d be some sums involved).
In a distribution like this, they all have the same value. But what happens when a distribution isn’t symmetrical, say, the same top and bottom point, but the bump slightly lower down? Well, then the most common waist size might not be the same as the average; like this.

Why is this relevant to selling knickers?
If you want to make sure that your stuff sells and as fast as possible, then you need to make it in the most popular sizes. Every season, we look at what sold last season, and adjust what we plan to make based on that. We can’t do great stats because our numbers are too small, but it helps.
You’d think from the original graph that that would mean that everyone should make lingerie mostly in a size 14-16, but as we all know, lots of brands don’t even do a size 16. Why not?
Well, firstly, it's quite likely that though that’s the arithmetic mean, it's not the most common size. I haven’t been able to get the stats for this, so I don’t know, but definitely for us, our graphs of what sells are skewed. That second graph, that’s what we mean by a skew. Wages follow this pattern, which is why you might find that everyone you know has a less than average income – the average wage doesn’t mean the same as the most common wage! For a slightly gruesome demonstration of the difference between the mode and the mean skewed the opposite way: most people have 10 fingers, so the mode is 10. But the average is less than that, due to a regrettable tendency on humanity’s part to stick their fingers in stupid places, plus fail to grow extras.
You can see that in these circumstances, if we made things in amounts that were symmetrical around the mean, we’d run out of the smaller sizes and be left with the bigger sizes sitting around.
Secondly, the people you sell to don’t necessarily have the same statistics as the population as a whole. If you take a whole bunch of small groups of people at random, on average, they’d have the same characteristics as the overall population (which is how census stuff and MORI polls and the like work, by the way). But your customers aren’t random. You may set out to appeal to a certain group – for example, Playful Promises is aimed at the 18-30 year old market, so their sizes run smaller than our because, as I know only too well, we tend to be smaller in our 20’s than our 30’s, and so on. We tend to sell to more mature women, so my sizing distribution is roughly the same shape as theirs, but the most popular sizes are a bit bigger, and we get more requests from much curvier people than Playful do.
(Edited to add; 10 years on this has changed! PP expanded and with it so did their requests and their ranges).
Equally, if you never do larger sizes or tiny sizes, then you never build a reputation with those communities, so your sample chooses itself. I do sometimes wonder whether this is how we arrive in a situation whereby what sells is much smaller than it statistically should be – having been deprived of fashionable clothing for ages, perhaps curvier women have just stopped bothering to shop?
You might ask why we can’t just make tiny quantities of the sizes on the far end of the distribution. The answer, as always, is money. Basically, the cost of one item goes down the more you do of them. So, keeping the sums simple, if you make one of a thing, it might cost you £10 to do (from an established pattern; developing patterns for new samples costs much, much more). If you make 100 of a thing, it’ll only cost you £2 per each one, because you can chop all the panels at the same time, do production lines, buy components in bulk, and so on. So factories don’t let you just make 5 or 10 of a thing unless you want to pay a lot extra, so you’d have to order enough to add 20-50% to your overall amounts – and your costs – for things that might not sell for a very long time. Ow.
If you’re a very big company producing tens of thousands of each item, then it’s less difficult, because the quantity it takes to add a few sizes is a much smaller percentage of the overall costs.
Bras sizes are . . . worse. For starters, there’s a ton of them. Secondly, when you’re as small as us you don’t get anything approaching a symmetrical distribution on the sales of bras, you get something like this:

Let's say the most we ever make of a range is 1000 (it's less than that, but multiples of 10 are where I’m at, sums wise). Say the minimum the factory will let us do is 50 of a size. That would give us 20 sizes we were allowed to do, and they’d have to be 20 sizes that all sold the same amount, ideally. That never happens, so to make the most of our money, we’d probably want to choose fewer sizes than that and make more B and C cups to meet demand. Let's say we choose 15 sizes – 32-36B-DD and 38C-DD, based on what we know people buy, and vary the amounts a bit based on which we know sells more or less.
Then imagine I say to the factory that we want to add E cups across the range. That would be a minimum of 200 extra bras. We were only making 1000 in the first place. We’ve just added 20% to our costs. Imagine we pay £10 each for the bras – that’s a bill that’s gone from £10,000 to £12,000 – and we’ll need to order extra knickers as well, so those costs go up too. Big ow.
If I tell the factory I want to add E, F and G cups, firstly, they will laugh in my face (and ask for a new pattern and the costs thereof, because our stuff doesn’t necessarily work for larger cup sizes and usually requires some bolstering), and secondly, because it’s a pain in the bum for them, they will tell me I need to add more than just the minimum amount overall – generally, to add 3 extra bra sizes they want me to add about 30% overall to the amount. So we’d have to more than double the overall amount of bras we order, plus extra bottoms to match, to add in 2 extra cup sizes.
GIANT OW. I don’t think we can double our sales in a season, particularly not in an area where we have no specialist retailers and no established customers.
Again, if we were a bigger company, all this would be a lot easier – we could do a push into a new market, negotiate with retailers, we could get a better deal from the factories, etc. Even the sums just make more sense, before you get into purchasing power and economies of scale. Back to that magic 68% that will cover most of the people in a size spread – 68% of 1000 bras only leaves you with 320 bras to cover all the less common sizes – or about 3 cups sizes because the factories don’t want to make less than 50. If you’re making 10,000 bras, then you’ve got 6,800 left to play with – 136 less common sizes you could think about doing, if you ask the factory nicely and they are ok with doing just 50 of each.
So that was very long. In summary, if we don’t do your size; its not you, it's us. We can’t afford you, dahling!